Hvor blir det av de nysgjerrige elevene?
Matematikk er kanskje det mest misforståtte faget på skolen.
At elever forbinder matematikk med et huskefag (Herheim, 2016), eller
som et fag der man ikke skal samarbeide eller tenke (Boaler, 2015) er
bare noen eksempler som indikerer det. Forskning viser at allerede før barn
begynner på skolen, har de en uformell matematisk
kunnskap som er overraskende bred, kompleks og avansert. Om man ser
på barn som leker, kan man observere at de utforsker mønster og former, de
sammenlikner størrelser og avstander og de har en viss forståelse for mengder (Clements &
Sarama, 2007). Hva skjer når barna begynner på skolen? Hvorfor klarer vi ikke å
ivareta den iboende nysgjerrigheten som barn har når de begynner på skolen?
Forskning
viser at dersom elevene lærer matematikk som et sett av isolerte prosedyrer som
skal pugges og huskes utenat, vil det føre til en begrenset matematisk
forståelse. For det første vil man ikke kunne dra nytte av prosedyrene hvis konteksten
endres, og for det andre er man låst fast hvis man ikke husker regelen
(Schoenfeld, mfl., 2014). Boaler viser et eksempel som illustrerer problemet
med å bare pugge regler og prosedyrer; en lærer ga et matematisk problem til
elevenes foreldre. Mange av de voksne som hadde lært matematikk på den
tradisjonelle måten var ikke i stand til å løse problemet. De viste at noe
skulle multipliseres, men husket ikke hva. Først etter at læreren hadde satt
opp likningen for dem, klarte foreldrene å løse problemet. Det som er interessant i dette eksempelet er at en elev som ikke hadde lært seg prosedyren enda, klarte
å løse problemet ved å tenke logisk (Boaler, 2015).
At matematikkundervisningen i stor grad handler om å pugge regler og prosedyrer som man bruker til å løse oppgaver som passer til den aktuelle regelen, er nok noe de fleste kan kjenne seg igjen i. Som lærer ønsker man at elevene skal føle mestring, få mulighet til å være kreative og nysgjerrige, samtidig som de skal utvikle matematisk forståelse og kompetanse. Ved å bare undervise tradisjonelt vil jeg si at vi frarøver elevene denne muligheten, noe som igjen kan føre til at de mister motivasjonen og gleden av matematikk. Det er på denne måten
vi mister de nysgjerrige barna som søker etter en forståelse av verden rundt. Kan vi undervise på en måte som gjør at elevene kan løse problemer uten å måtte pugge titals regler?
Læring og undervisning
Geometri
 På nivå 0 forholder barn seg til et begrenset
antall figurer uten å ha bestemt navn på dem. For eksempel ser vi at små barn
kan sette puzzle brikker på rett plass, eller at de klarer å putte geometriske
treklosser i riktig åpning på boksen. På nivå 1 bygger elevene på gjenkjennelse
av figuren som helhet og ikke på vurdering av figurens egenskaper. For eksempel
vil en elev som bare har sett kvadrater i ”standardposisjon”, ha vanskeligheter
for å kjenne kvadratet igjen i andre posisjoner (se figur 2).
På nivå 0 forholder barn seg til et begrenset
antall figurer uten å ha bestemt navn på dem. For eksempel ser vi at små barn
kan sette puzzle brikker på rett plass, eller at de klarer å putte geometriske
treklosser i riktig åpning på boksen. På nivå 1 bygger elevene på gjenkjennelse
av figuren som helhet og ikke på vurdering av figurens egenskaper. For eksempel
vil en elev som bare har sett kvadrater i ”standardposisjon”, ha vanskeligheter
for å kjenne kvadratet igjen i andre posisjoner (se figur 2).
På nivå 2 er
eleven opptatt av egenskapene til figuren, for eksempel at rektangler har rette
vinkler. På dette nivået vil de ikke kunne resonnere seg frem til at ”alle
rektangler har rette vinkler” medfører at ”alle rektangler har parvis
parallelle sider”. Nivå 3; eleven kan se sammenhenger mellom ulike egenskaper
til en figur og mellom forskjellige figurer. På nivå 4 begynner eleven å
utvikle kunnskap om definisjoner, aksiomer og teoremer, og de klarer å etablere
geometriske bevis. På det siste nivået, nivå 5, kan elevene forklare formelt om
geometriske systemer (Battista, 2007). Forskning viser at elevene ligger
på et lavt nivå i geometri, og at elever som regel ikke kommer seg lenger enn
til nivå 3 i løpet av ungdomsskolen (ibid.).
Problembasert
undervisning
Det som kjennetegner problembasert undervisning er at
elevene skal inkluderes i læringen og de skal få oppgaver som utfordrer dem.
Det fins ulike definisjoner på hva problemløsning er. Lesh & Zawojewski
(2007, s.782) definerer problemløsning slik; ”en oppgave er et problem når den
som skal løse problemet må utvikle mer produktive måter å tenke på om den gitte
situasjonen”. En annen definisjon er av problemløsning er å se det som en
kognitiv prosess rettet mot et mål, der løsningen eller løsningsprosessen ikke
er åpenbart for problemløseren (Powell, mfl., 2009, s.134). Polya har beskrevet
fire steg i arbeidet med problemløsning;
- Forstå problemet
- Lag en plan
- Gjennomføre planen
- Se tilbake på resultatet - vurder og diskuter.
For at læreren skal utvikle gode problemløsere i klassen
sin, kan det kreve en del i starten. Læreren må få elevene interessert i
problemet, og elevene må få tid til å øve seg på å finne strategier for å løse
problemet (Polya, 2013). Oppgavene må også være designet slik at nivået for å
klare å starte på problemet er lav, men at problemet samtidig kan utvikles til
å nå høyere nivå etter hvert. Det er dette som betegnes som ”low floor, high ceiling”
(Sullivan mfl.,2015).
Det er også viktig å huske på at et problem er noe som er individuelt – det som
er et problem for en elev, trenger ikke å være et problem for en annen.
Undervisningsopplegg
Elevene vil også kunne komme inn på
følgende kompetansemål fra Måling etter 10.årstrinn:
Materiale:
Introduksjon
I tillegg til å se sammenhengen
mellom arealet av grunnflaten og høyden i sylinderen, ønsker jeg at elevene
skal bruke matematiske begreper som er hensiktsmessig for dette problemet, for
eksempel sylinder, volum, grunnflate, areal, høyde..
Oppgave som gis til elevene:
Avslutningsvis er det viktig at man
tar opp de strategiene som er kommet frem i løpet av undervisningen. Dette kan
gjerne gjøres i en felles klassediskusjon.
----------------------
Det kan virke som at tradisjonell
undervisning regnes som dårlig undervisning, mens undervisningsmetoder som problembasert
undervisning regnes som god undervisning. Jeg tenker at man må vurdere hver
undervisningsøkt, og tenke nøye igjennom hva som vil være mest hensiktsmessig
for at elevene skal lære. Noen ganger kan
det hende at en regel vil være den beste måten å lære på, mens andre ganger vil
elevene få størst utbytte gjennom å selv være aktive i læringsprosessen. Alle
elevene er forskjellige og har ulike tilnærminger til kunnskap. Uansett hvilken
undervisningsmetode som velges, mener jeg at å snakke matematikk - hvor man får
brukt begreper, argumentert for strategier og metoder og reflektert over svar,
er viktig for læringen.
Kilder:
Battista,
M. T. (2007). The development of
geometric thinking and spatial thinking. I F. K. Lester, . Second
handbook of research on mathematics teaching and learning. (s. 843-908).
Charlotte, N. C.: Information Age
Boaler, J. (2015). The Elephant in the classroom - helping
children learn and love maths.
Clements, D. H., & Sarama, J. (2007).
Early Childhood Mathematics Learning. I F. K.
Herheim, R. (2016). Matematikk som magi
- hugsereglar og konsekvensar.
Lesh, R. & Zawojewski, J.
(2007). Problem solving and modeling. I F.K. Lester, Second
handbook of research on mathematics teaching and learning.
Polya, G. (2013). How to Solve It.
USA: Stellar Books.
Skemp, R. R. (1976). Relational
Understanding and Instrumental Understanding Mathematics teaching.
Utdanningsdirektoratet. (2013). Læreplan
i matematikk - føremål. Hentet 10 14, 2017 fra
https://www.udir.no/kl06/MAT1-04/Hele/Formaal
Utdanningsdirektoratet. (2013). Læreplan
i matematikk. Hentet 10 13, 2017 fra
https://www.udir.no/kl06/MAT1-04/Hele/Kompetansemaal/kompetansemal-etter-10.-arssteget.
Scoenfeld, A. H., Floden,
R. E., & the Algebra Teaching Study and Mathematics Assessment Project
(2014). An introduction to the TRU Math Dimensions. Berkeley,
CA & E. Landing, MI: Graduate School of Education, University of
California, Berkeley & College of Education, Michigan State University.
Film:
Youtube.com, What is PBL? Problem based learning.
 På nivå 0 forholder barn seg til et begrenset
antall figurer uten å ha bestemt navn på dem. For eksempel ser vi at små barn
kan sette puzzle brikker på rett plass, eller at de klarer å putte geometriske
treklosser i riktig åpning på boksen. På nivå 1 bygger elevene på gjenkjennelse
av figuren som helhet og ikke på vurdering av figurens egenskaper. For eksempel
vil en elev som bare har sett kvadrater i ”standardposisjon”, ha vanskeligheter
for å kjenne kvadratet igjen i andre posisjoner (se figur 2).
På nivå 0 forholder barn seg til et begrenset
antall figurer uten å ha bestemt navn på dem. For eksempel ser vi at små barn
kan sette puzzle brikker på rett plass, eller at de klarer å putte geometriske
treklosser i riktig åpning på boksen. På nivå 1 bygger elevene på gjenkjennelse
av figuren som helhet og ikke på vurdering av figurens egenskaper. For eksempel
vil en elev som bare har sett kvadrater i ”standardposisjon”, ha vanskeligheter
for å kjenne kvadratet igjen i andre posisjoner (se figur 2). 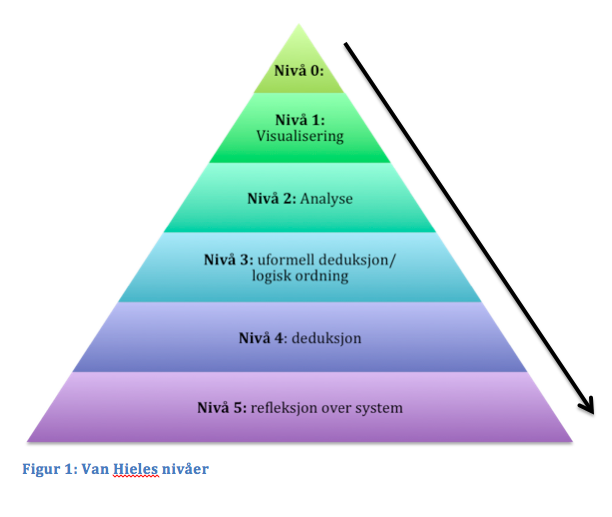

Kommentarer
Legg inn en kommentar