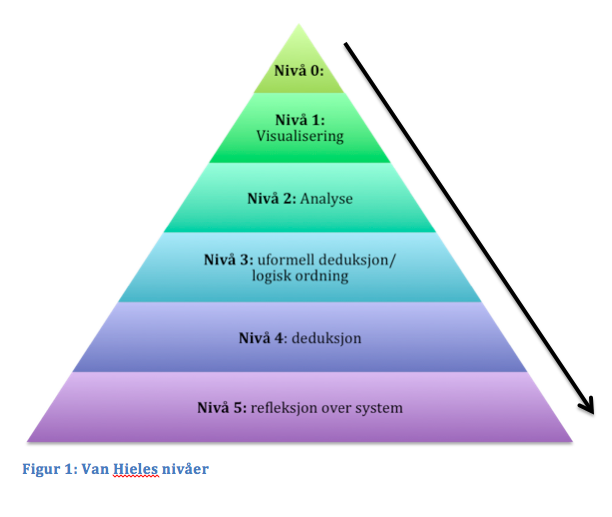
Hvordan plenumssamtalen kan gi økt forståelse i arbeidet med funksjoner

Dette blogginnlegget tar for seg hvordan plenumssamtalen i matematikkundervisningen kan gjennomføres for legge til rette for en dypere forståelse for sammenhenger mellom representasjoner av lineære funksjoner. I likhet med Skemp definerer jeg forståelse i matematikken i to former; instrumentell og relasjonell. Å ha instrumentelle forståelsen kan kort beskrives ved at man kan gjennomføre innøvde regnestrategier uten å forstå hvorfor det blir rett. Skemp beskriver dette som rules witout reasons (Skemp, 1986). Eleven vil derfor ha vanskeligheter med å benytte seg av det matematiske innholdet i et problem eller utfordring, da det er en mangel på bevissthet om hvordan trinnene i de ulike instruksjonene henger sammen. Skemp forklarer dette med at eleven ikke har utviklet et passende skjema (Ibid). Hvis man har relasjonell forståelse, så vet man både hva skal gjøres og hvorfor. Her mener Skemp at e leven har etablert et godt skjema, som vil gjøre eleven ...