Problemløsning i Geometri!

Hvor ofte satt du ikke og regnet matematikk i skriveboken din når du gikk på skolen? Er du av den samme oppfattelsen som meg om at matematikktimene primært besto av at læreren «foreleste» på tavlen, før diverse oppgaver skulle løses i skriveboken med en forutbestemt prosedyre?

Problemløsning:

I Ludvigsenutvalgets anbefaling til regjeringen angående fremtidens skole poengteres det at problemløsning er et av flere områder det må satses mer på i skolen i årene som kommer.(NOU 2015:8)

Problemløsning er en elevaktiv arbeidsmetode der elevene kan arbeide i grupper eller individuelt med ulike oppgaver. Problemløsning som metode kan benyttes på ulike måter, ved at en for eksempel bruker en hel eller flere undervisningsøkter på å arbeide med denne aktive arbeidsmetoden, eller ved at en kun bruker en del av undervisningsøkten. Elevene kan arbeide selvstendig eller i grupper med ulik grad av samarbeid og involvering av lærer. De ulike oppgavene som skal arbeides med kan lages av læreren selv. En problemløsningsoppgave er en oppgave som er utforskende for eleven. Altså at eleven må prøve seg fram til en endelig løsning. I utformingen av problembaserte oppgaver presiseres det at lærerens kompetanse på spesielt to ulike områder er viktig for å kunne lage en god oppgave. Disse punktene er «Spesialisert matematisk kunnskap» og «kunnskap om innhold og undervisning».(Sullivan P., Knott L., Yang Y. 2015) De to nevnte er to av seks kunnskapsformer som Ball beskriver som nødvendige for å undervise i matematikk. Spesialisert kunnskap er matematisk kunnskap knyttet til kun det å undervise.  Det som menes med dette er at lærere har en litt annen tilnærming til matematikk som fag enn for eksempel ingeniører, da lærere må se etter mønstre hos elever for å detektere feil og misoppfatninger. Kunnskap om dette er da viktig for å konstruere en god oppgave. Kunnskap om innhold og det å undervise handler om at læreren er nødt til å gjøre valg i forbindelse med hva som for eksempel skal presenteres for elevene i starten av et nytt emne og hva som skal etterlates til elevenes kognitive arbeid. (Ball, 2008)

I tillegg til lærerens kompetanse på de to ovennevnte områdene vektlegges det at oppgavenes kontekst må treffe elevene, altså at oppgavene må være tilrettelagt slik at elevene kan kjenne seg igjen i dette. Freudenthals realistiske matematikk (RME) går ut på akkurat dette. Matematikken som skal arbeides med må presenteres i en kontekst som er kjent slik at det skapes en arena for elevenes aktivitet. Konteksten trenger ikke å være en konkret hendelse eller objekt, det kan også være mer abstrakt og fantasifull situasjon. Hovedpoenget er at opplegget skal presentere en situasjon som elevene kan forestille seg og føle seg en del av. (Skott, Jess, & Hansen, 2016)

I utarbeidingen av problemløsningsoppgaver beskrives det fem ulike dilemmaer som må taes hensyn til. De ulike dilemmaene er kontekst, språk, struktur, fordeling og nivåer av interraksjoner. Disse ulike dilemmaene kan også brukes for å vurdere en eksisterende oppgave.(Sullivan P., Knott L., Yang Y. 2015)

Når elevene skal jobbe med matematikk ved hjelp av problemløsning kreves det at de innehar noen forhåndskunnskaper om ulike matematiske begreper. Dette fordi at i arbeidet med å lage en plan over hvordan oppgaven skal gjøres så må man ha noen teknikker eller tidligere erfart kunnskap som en kan prøve å benytte seg av. George Pólya beskrev fire steg i arbeidet med problemløsning. (Pólya, 1945)

Pólyas fire steg i problemløsning.

Det første steget består i å forstå hva som er problemet. Dette kan for eksempel gjøres ved å dele opp problemstillingen i flere mindre deler slik at problemet ikke virker for komplekst.

Det andre steget i Pólyas modell består i å lage en plan for å finne ut av problemet. Er det noe du tidligere har erfart? Finnes det noe av din tidligere erfarte kunnskap som kan brukes for å løse problemet?

I det tredje steget utfører du planen som du la i steg to. Her er det viktig at du kontrollerer at du gjør det riktig på hvert steg som du planla i trinn to.

Det fjerde og siste steget i modellen er å se tilbake på resultatet og problemet. Er svaret samsvarende med problemstillingen? Ulike refleksjoner knyttet til oppgaven gjøres da i dette trinnet.

Noe som kan fremme en positiv opplevelse av problemløsningsoppgaver er hvis oppgaven kan beskrives som «low floor, high ceiling», det vil si at terskelen for å starte på oppgaven er lav men samtidig kan oppgaven utvikles til et mye høyere nivå enn det som kreves for kun å starte på denne. (Sullivan P., Knott L., Yang Y. 2015)

Problemløsning kan kanskje høres ut som det perfekte undervisningsmiddelet for å la elevene utfolde seg kreativt og dermed knytte kunnskapen til noe de selv har erfart og dermed kunne utvikle konseptuell forståelse i faget. I teorien høres slike oppgaver veldig positive ut, men jeg sier ikke at lærere kun skal undervise på denne måten. Det kan være elever som får et bedre utbytte av timene ved å regne på den gode gamle måten enn ved å løse oppgaver problembasert. I tillegg til at elevenes læringsutbytte kan variere er det flere faktorer som kan påvirke om en klarer å gjennomføre slike oppgaver. Lærerens kompetanse, rammefaktorer i klasserommet som plass, tid etc.

Poenget mitt er ikke at en må ta et standpunkt om en skal undervise med eller uten problemløsning, men at det finnes en mellomting. Å bruke litt problemløsning i faget er bedre enn ingen bruk av dette.

Van Hieles nivåer i geometri:

Geometri kan sees på som et nettverk av begreper, resonnementer og representasjoner som brukes for å utforske og analysere rom og form. Geometri har opp gjennom historien hatt stor plass i skolen, og emnet har blitt sett på som et eksempel på hva matematikk virkelig er. Innen emnet geometri har diverse forskning blitt enige om at Van Hieles teori om elevers utvikling i geometri er en presis beskrivelse. Van Hieles modell beskriver hvordan barn lærer geometri gjennom flere kvalitativt adskilte nivåer. De ulike nivåene hierarkisk oppbyggd slik at elevene må gå gjennom et trinn for å komme til neste. 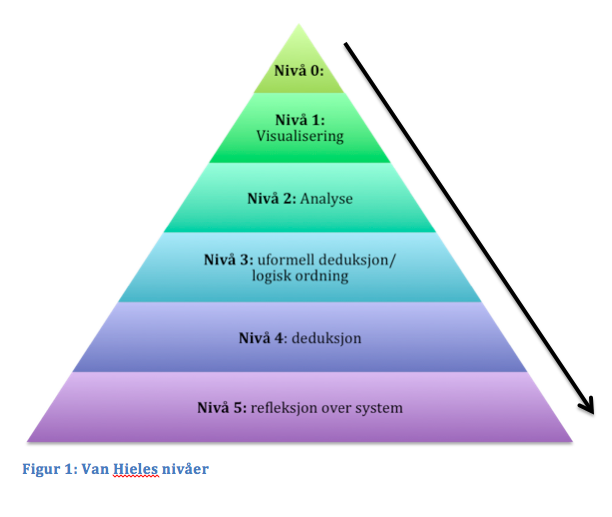Uavhengig av alder begynner barn på nivå 0 og beveger seg deretter oppover etter hvert som de lærer og erfarer geometri.(Battista) Figuren under viser de ulike nivåene i Van Hieles modell.

Figur 1: Van Hieles modell over forståelse i geometri.  Hentet fra https://ylgarris.wordpress.com/2013/07/15/the-van-hiele-levels-of-gemetric-understanding/

I det første nivået i modellen kan elever identifisere figurer slik som kvadrat, rektangel, trekant osv. Elevene fokuserer på hvordan figuren ser ut og ikke dens egenskaper. Nivå 1: Analysen kjennetegnes ved at elever begynner å fokusere på sentrale egenskaper til figurer. De kan gi en liste av egenskaper som hører til f.eks et kvadrat men vet ikke hvilke som er nødvendige og hvilke som er tilstrekkelig. På nivå 2 kan elever se sammenhengen mellom forskjellige egenskaper til en figur og mellom forskjellige figurer. Elevene kan her begynne å følge uformelle bevis. Nivå 3 handler om deduktive systemer, fokus her er enkle beviser og elevene får et visst grep om definisjoner, aksiomer og teoremer. Det siste nivået, nivå 4 er geometri på profesjonelt nivå, altså slik matematikere forstår og arbeider med geometri. Man kan sammenligne forskjellige geometriske systemer. Undervisningsopplegget som er beskrevet i denne bloggen krever at elevene er på slutten av nivå 1, analyse. Oppgavens hensikt er å bidra til elevenes forståelse om egenskaper til figurene. For utdyping av nivåene 0-2 se video under.

Bruken av konkreter:

Bruken av konkreter som elevene kan benytte seg av i matematikkfaget er sikkert kjent for mange. Du har kanskje brukt brikker på skolen når du arbeidet med divisjon? I geometri har du kanskje brukt ulike figurer og modeller for å faktisk se å forstå formen og dermed de ulike geometriske egenskapene til figuren. Moyer presiserer i sin artikkel at bruken av konkreter ikke nødvendigvis gir konseptuell forståelse. Det er først når konkretene settes i sammenheng med det som skal læres og når de kan sees på som en helhet i arbeidsøkten sammen med temaet at de gir mening. Altså når elevene ved å benytte seg av konkreter utvikler egne ideer skaper de matematisk forståelse. Utfordringen for lærere er altså å bruke riktig verktøy til den nødvendige jobben. (Moyer, 2001) Dette krever erfaring og ulik kompetanse hos læreren. Slik kompetanse kan knyttes mot de to ulike kompetansene som ble nevnt tidligere av Ball. Det å bruke konkreter bare for å bruke det har altså liten hensikt for elevenes læring.

  

Undervisningsopplegg:

Oppgaven tar for seg tre ulike geometriske figurer. Elevene skal finne ut av arealet og volumet til en av de tre figurene som er valgt av læreren på forhånd. Opplegget er tenkt for 6-7 trinn. Elevene skal ikke regne ut arealet og volumet til alle tre figurene men velge seg en de vil arbeide med. Det antas at dette opplegget varer i ca 45-60 minutter.

Læringsmål: Forstå begrepene areal og volum til en tredimensjonal figur.

Utstyr som kreves: to ulike typer prismer, en med rektangulær form, en med form som trekant. I tillegg til de to ulike prismene trengs en sylinder. Lengden på prismene og sylinderen må være den samme. Kubikkcentimeterkuber, kvadratcentimeterbrikker, beger til å ha vann i, kjøkkenvekt, kalkulator, blyanter og papir.

Figur 2: De ulike geometriske figurene elevene skal arbeide med

Elevene skal arbeide i grupper på 3 elever, her velger læreren ut hvilke elever som skal arbeide sammen. Dette for å gå satt sammen grupper som kan utfordre og utvikle hverandre. De ulike gruppene velger hvilke geometriske figurer de ønsker å ta for seg, dersom en gruppe ønsker å ta for seg sylinderen får de da gjøre dette. Avslutningsvis skal elevene prøve å sette opp standardformelen for areal og volum til den valgte figuren.

Elevene må sammen i gruppene deretter gå sammen og hva som skal gjøres på de ulike figurene. Hva som burde finnes først og hvordan framgangsmåten for de ulike egenskapene er. De må altså benytte seg av Polyas fire trinn i problemløsning, her kan læreren være behjelpelig med å strukturere arbeidsprosessen til elevene ved å gi dem råd.

Valget av de ulike geometriske figurene er ikke tilfeldig. Dersom en gruppe velger å ta for seg prismet som er formet som et rektangel først og fullfører arbeidet med denne figuren tidlig i økten kan gruppen avansere til en av de andre geometriske figurene. Arealet og volumet til de ulike figurene vil delvis være like da lengden bakover i planet er lik på alle figurene. Overføring av kunnskap fra en geometrisk form til en annen vil altså være mulig i arbeidet med figurene.  

Elevene har konkreter tilgjengelig slik som brikker som dekker 1 kvadratcentimeter og kuber som er på 1 kubikkcentimeter. Disse konkretene kan elevene benytte seg av fritt i oppgavene, men det er kun i arbeidet med den ene prismen at de klarer å få til et presist svar ved å benytte seg av disse. De kan dermed gi en pekepinn på hvor stort arealet og volumet er på de to andre geometriske formene men mer avanserte kognitive strategier er nødvendige for å få til et presist svar. Når det kommer til bruken av vann og vekt knyttet mot volum er dette noe elevene står fritt til å disponere. Det kreves derimot at elevene har kunnskaper angående volum om at 1 liter vann veier 1 kg. Denne kunnskapen sitter mest sannsynlig ikke hos alle elevene og det vil derfor ikke være alle gruppene som benytter seg av dette. Opplegget legger opp til at elevene kan bruke forskjellige strategier på bakgrunn av hvilke erfaringer og hvilken kunnskap de allerede innehar for å løse problemene.

Referanser

Ball, D. L. (2008, 11 1). Content Knowledge for Teaching - What makes it special? Journal of Teacher Education. Henta frå http://journals.sagepub.com/doi/abs/10.1177/0022487108324554

Pólya, G. (1945). How to solve it - A new aspect og mathematical method. Penguin books.

Skott, J., Jess, K., & Hansen, H. C. (2016). Matematikk for lærerstuderende - Delta. Frederiksberg: samfundslitteratur.

 St.meld. nr. 8 (2015. Fremtidens skole – Fornyelse av fag og kompetanse. Hentet fra https://www.regjeringen.no/no/dokumenter/nou-2015-8/id2417001/

Battista, M. (). The Development of geometric and spatial thinking. I Second handbook of research on mathematics teaching and learning (ss. 843-908).

Sullivan P., Knott L., Yang Y. (2015) The Relationships Between Task Design, Anticipated Pedagogies, and Student Learning. In: Watson A., Ohtani M. (eds) Task Design In Mathematics Education.

Moyer, P.S. Educational Studies in Mathematics (2001) 47: 175. https://doi.org/10.1023/A:1014596316942

Theory of Geometric Thinking Hentet fra Youtube.com https://www.youtube.com/watch?v=SykgOciBFsk