Gi elevene mer engasjerende og motiverende undervisning!
Kandidat 11 og 21
For elevene kan matematikkundervisningen virke lite varierende og motivasjonen er kanskje ikke helt på topp. I den norske skolen oppleves undervisningen som tradisjonell, der det er læreren som styrer undervisningen og den er påvirket av hvilke lærebøker/læremateriell h*n velger å benytte. Læreren gjennomgår lærestoff på tavla, elevene arbeider med oppgaver knyttet til det læreren har gjennomgått, for deretter å ha en oppsummering på slutten av timen. Dette undervisningsforløpet kjenner de fleste elevene seg igjen i. Så hvordan kan man skape en engasjerende og motiverende undervisning?
Det er stadig diskusjoner om hvordan undervisning i matematikk burde være. Man er opptatt
av hvordan elevene skal lære og hva som er den beste fremgangsmåten for å få dette til;
hvilke arbeidsmetoder som er den beste. Det kommer stadig ny forskning, og det blir flere
ulike begreper å forholde seg til, dette er fordi flere ønsker å vise til hvordan undervisningen
bør legges opp i matematikk. Problemløsning har blitt en sentral del av matematikken, hvor bruk av matematisk problemløsning i klasserommet har blitt et stort tema innenfor forskning. Flere forskere mener at elevene bør bli utfordret og få muligheten til å arbeide med problemløsning i skolen (Schoenfeld mfl., 2007). Også i Norge er problemløsning blitt et voksende tema, det kan vi blant annet se i skolereformen Kunnskapsløftet. Læreplanverket for matematikk viser blant annet til at opplæringen i matematikk skal veksle mellom utforskende, lekende, kreative og problemløsende aktiviteter og ferdighetstrening (Utdanningsdirektoratet, 2013).
Med dette blogginnlegget ønsker vi å rette lyset på hva som er god undervisning i matematikk og presentere et undervisningsopplegg som vi mener faller innenfor dette. Undervisningsopplegget vil ta utgangspunkt i at elevene skal jobbe med en problemløsende oppgave innenfor tematikken geometri.
Hva er god undervisning i matematikk?
For å få en god undervisning i matematikk er det viktig å være klar over hvordan elevene
lærer og forstår matematikk. Richard Skemp (1976) forklarer hvordan man forstår
matematikk i begrepene relasjonell og instrumentell forståelse. Det handler hvorvidt en elev
har forståelse for hva han gjør. En instrumentell forståelse vil si at elevene kan beherske
regler/prosedyrer, men for en som har denne forståelsen vil ikke kunne forklare eller forstå
hvorfor disse reglene/prosedyrene fungerer. Derimot vil en som har en relasjonell forståelse
for matematikk kunne forklare hvordan og forstå hvordan regler/prosedyrer fungerer, siden
eleven ikke vil være avhengig av disse reglene/prosedyrene som en elev som har
instrumentell forståelse har.
Innenfor matematikkdidaktikk har det blitt utviklet flere teoretiske rammeverk som beskriver
undervisning og læring i matematikk. Teaching for Robust Understanding in Mathematics
(Tru Math) er et et slikt teoretisk rammeverk (Schoenfeld, mfl., 2014). Tru Math er et
analytisk rammeverk som skal kunne forbedre læringen i klasserommet ved å utvikle en dypere forståelse av læring og hvordan man kan berike undervisningen (Schoenfeld mfl., 2016). Rammeverket er karakterisert av 5 overlappende og viktige dimensjoner av undervisningen som skjer i klasserommet. Disse 5 dimensjonene vises i Bilde 1, men vi skal kort forklare hva de forskjellige dimensjonene forteller.
Bilde 1: Five dimensions of mathematically powerful classroom
|
Den første dimensjonen, The Mathematics, ser på hvordan elevene erfarer matematikk. Om
matematikken blir sett på som sett av isolerte fakta, prosedyrer og konsepter som blir øvet,
memorert og brukt, kan dette forstås som instrumentell forståelse. Dersom matematikken blir
erfart som sammenhengende, der prosesser og prosedyrer er meningsfulle og forstående for
elevene, forstår vi dette som relasjonell forståelse.
Den andre dimensjon, Cognitive demand, ser på om elevene har muligheten til å bli utfordret
slik at det gir rom for og hjelp til deres utvikling av matematisk forståelse.
Den tredje dimensjonen, Access to the Mathematical Content, viser til hvem det er som får
delta i aktivitetene og diskusjonene. Alle elevene bør bli involvert på en meningsfull måte,
hvor aktivitetene i klasserommet skal inviterer og støtte til aktivt engasjement.
Den fjerde dimensjonen, Agency, Authority and Identity, ser på i hvilken grad elevenes
matematiske ideer kommer til uttrykk i klasserommet. Blir ideene snakket om
eller bygget videre på av dem selv eller av andre?
Den siste dimensjonen, Uses of Assessment, handler om hvorvidt lærerne klarer å innhente
elevenes tenkning og responderer på de ideene som elevene gir. Klarer lærerne å møte
elevene hvor de er, og gir dem muligheten til å utvikle og utdype deres forståelse.
Innenfor hver av de 5 dimensjonene er det tre nivåer som beskriver
kvaliteten ved læringsmiljøet i klasserommet. For hvert nivå får man en «score», og det er
denne «scoren» som har betydning for kvaliteten for læringsmiljøet. Forskning viser at de
elvene som gjør det bra på tester som omhandler matematisk forståelse, tenkning og
problemløsning, er i et læringsmiljø som konsekvent «scorer» høyt i Tru Math (Schoenfeld
mfl, 2014). Vi oppfatter dermed at et klasserom som «scorer» høyt innenfor rammeverket har
tilrettelagt for at elevene skal kunne tilegne seg en relasjonell forståelse av matematikk.
Et gjennomgående tema i Tru Math er problemløsning, der rammeverket mener at elevene
bør ha muligheten til å engasjere seg i problemløsning. Et formål Tru Math har er
et lærere kan bruke rammeverket til å bli bedre på å skape et læringsmiljø hvor de 5
dimensjonene er representert på et høyt nivå. Dette kan bidra til at elevene blir bedre
matematiske tenkere og utvikle problemløsningsstrategier (Shoenfeld, mfl., 2014).
Problemløsning
Lesh & Zawojewski (2007, s. 782) definerer problemløsning som:
“A task, or goal-directed activity, becomes a problem (or problematic) when the “problem solver” (which may be a collaborating group of specialists) needs to develop more productive way of thinking about the giving situation”
Vi ser tilbake til scenarioet som ble gitt tidligere om hvordan elevene opplever undervisningen i skolen. De aktivitetene og oppgavene som elevene møter i det “tradisjonelle klasserommet” er gjerne knyttet til løsningsmetoder som allerede er kjent for dem. Det å arbeide med matematiske problemløsningsoppgaver eller aktiviteter vil si at løsningsmetoden ikke er kjent, og det kan gjerne være flere løsningsmetoder.
Lesh og Zawojewski (2007) ser på problemløsning som viktig for å kunne utvikle forståelse for et gitt matematisk konsept eller matematisk prosess. Dette er nok fordi at en gjennom problemløsning må gjennom en prosess der en først identifiserer problemet, utvikler ulike alternative løsninger og velger ut det beste alternativet en kommer fram til. For så å implementere dette alternativet og deretter vurdere om denne løsningen fungerer eller ikke. Denne prosessen illustreres i Bilde 2.
Bilde 2: Steps to solve a problem
|
Derfor må forskningsstudier av problemløsning, i følge Lesh og Zawojewski (2007), skje i sammenheng med å lære matematikk (og omvendt), dette er fordi det er forskjell på problemløsning gjort av nybegynnere og noen som har erfaring med det. Elevenes erfaringer med problemløsning har betydning for de adferdene de gjør og hvordan de tolker en problemsituasjon på. Forskningen må også fokusere på elevenes tolkninger, representasjoner og refleksjoner, samt beregningene de utfører, resonnementene de bruker, ferdighetsnivået de utvikler og regler og prosedyrer som de lærer å utføre. Dette viser altså at det er et samarbeidende forhold mellom læring og problemløsning, og med bakgrunn i dette tenker vi at problemløsning er viktig i skolen for at elevene skal utvikle sine tolkninger, representasjoner og refleksjoner i matematikk.
Geometri
Geometri er et stort emne i matematikk, som har betydning for matematisk teori og anvendelse (Battista, 2007). Til tross for dette, har studentene vanskeligheter med å lære geometri i dybden. Battista (2007) viser at elevenes læring er påvirket av dårlig forståelse av geometriske mål, der det spesielt dreier seg som misoppfatninger om lengder.
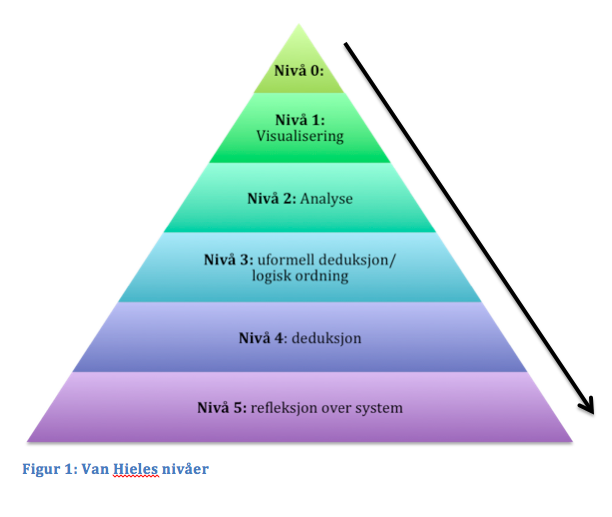
Van Hiele-teorien viser elevenes utvikling av geometrisk tenking gjennom 6 nivåer, fra nivå 0 til nivå 5 (Battista, 2007). Disse nivåene er sekvensielle og hierarkiske, som vil si at dersom en elev skal kunne nå det neste nivået, må de ha mestret de tidligere nivåene. Nedenfor presenteres de ulike nivåene i en tabell vi har utarbeidet, inspirert av Van Hiele-teorien.
| Tabell 1: Nivåene i Van Hiele-teorien |
Forskning viser at elevene generelt ligger på lave nivåer innenfor geometrisk tenking (Battista, 2007). Ved at elevene ligger på slike lave nivåer kan dette gi dårlige forutsetninger for å mestre nye emner senere i livet. Som nevnt, viser forskning at elevene har vanskeligheter ved å lære geometri i dybden. Hvilke oppgaver som elevene får i undervisningen, har mye å si for deres læring og forståelse. For at vi som lærere skal kunne fremme en relasjonell forståelse og få elevene til et høyere nivå innenfor geometrisk tenking, bør vi gi dem oppgaver som kan stimulere til dette. Ut i fra van Hiele-teorien oppfatter vi at geometri er et emne som har gode muligheter for å arbeide med utforskende og problemløsende oppgaver. Derfor har vi tatt utgangspunkt i en problemløsende oppgave i geometri for undervisningsopplegget.
Undervisningsopplegget
Undervisningsopplegget tar utgangspunkt i den problemløsende oppgaven “Finding the shortest route: A schoolyard problem”. Dette opplegget er hentet fra MARS (Mathematics Assessment Resource Service) og er utviklet i forhold til det teoretiske rammeverket Tru Math.
Undervisningsopplegget er tenkt til å gjennomføres på en ungdomsskole, og tar derfor utgangspunkt i følgende kompetansemål fra K06 etter 10. årstrinn:
“Utforske, eksperimentere og formulere logiske resonnementer ved hjelp av geometriske ideer”
“Bruke og gjengi bruken av formlikhet og Pytagoras`setning i beregning av ukjente størrelser”
(Utdanningsdirektoratet, 2013).
Målet for denne økten vil dermed være at elevene utvikler/tilegner seg kunnskap og forståelse for Pytagoras` setning og hvordan man kan benytte seg av denne til å løse problemer i hverdagen. I tillegg vil elevene også kunne utvikle sine kunnskaper og metoder knyttet til ulike tilnærminger av problemløsning. Vi tenker oss at undervisningsøkten vil foregå på 9.trinn og er tiltenkt til å vare i totalt 90 min, altså to skoletimer á 45 minutt.
Oppgaven ”Finding the shortest route: a schoolyard problem” er som følgende:
Bilde 3: “The schoolyard problem”
|
Noen elever leker en lek i en rektangulær skolegård ABCD, som er 16 m x 12 m.
Elevene starter ved punktet S, som er 4 m langs den 16 m lange veggen AB.
De skal løpe og berøre de tre andre veggene, for deretter å returnere til startpunktet(S).
Den første som returnerer til S vinner leken.
Hva er den korteste ruten for dem å løpe?
Forklar hvordan du vet at denne er den korteste ruten å løpe.
Introduksjon til oppgaven:
På forhånd av undervisningsøkten skal elevene prøve å løse problemet individuelt. Ved å gi elevene oppgaven på forhånd vil man som lærer få mulighet til å vurdere elevenes arbeid og se hvilke utfordringer de har med oppgaven. Dette gjør at en kan gi mer effektiv og målrettet hjelp i matematikktimen. Elevenes oppgaver blir samlet inn, der læreren noterer ned hva elevenes arbeider avslører om deres nåværende nivå av forståelse og hvilke problemløsende strategier de benytter seg av. For å hjelpe elevene videre kan en nå lage en oversikt med spørsmål som kan hjelpe dem fra det utgangspunktet de har i oppgaven.
Undervisningsøkta:
I starten av økta benyttes 10 minutter til introduksjon av oppgaven i fellesskap der bilde av oppgaven tas opp på tavla, for å påminne elevene om oppgaven. De skal så beskrive oppgaven for sidekameraten, slik de husker det. Deretter bes noen elever (som en vet har ulike løsninger) komme opp på tavla for å tegne sin løsning på problemet, på denne måten får en presentert ulike løsningsforslag og elevene starter å reflektere rundt de ulike løsningene. Når en har noen ulike løsningsforslag tegnet opp spør en klassen om hvilken rute som er den korteste, og hvorfor den er det. På dette stadiet ønsker man ikke at en skal begynne å måle eller gjøre beregninger, men at elevene starter å reflektere intuitivt om hvilke ruter de tror kan være den korteste. Forhåpentligvis er det uenighet i klassen, noe som danner grunnlag for ytterligere diskusjon og refleksjoner. Det neste elevene skal gjøre er å igjen arbeide individuelt med oppgaven, og ved å sammenligne ulike tilnærminger prøve å komme fram til den korteste ruten. Elevene skal jobbe ca. 15 minutter individuelt, spørsmålene en har laget i forkant av timen tas opp på tavla slik at elevene kan benytte disse til å reflektere rundt sin egen løsning og evt. gjøre endringer på denne. Gjør elevene endringer tegnes dette inn med en annen farge enn den første løsningen deres.
Deretter plasseres elevene i grupper på 2-3 stk, der så langt det er mulig dannes grupper av elever med ulike løsningsforslag. I 15 minutter skal elevene arbeide i gruppene og forklare hva de har tenkt og gjort for å komme fram til akkurat det løsningsforslaget de har, samt sammenligne deres tilnærminger og identifisere tilnærmingenes fordeler og ulemper.
Det settes så av 20 minutter til at elevene innad i gruppene skal samarbeide om å gjøre en analyse av tre ulike tilnærminger som de får utdelt av læreren. Disse tilnærmingene er tre ulike løsningsforslag til oppgaven, som elevene skal benytte til å se hvilke likheter og ulikheter det er mellom tilnærmingene og det elevene selv har gjort. De skal også sammenligne de ulike tilnærmingene og se på fordeler og ulemper det er ved hver av disse.
Elevene får så 15 minutter til å lage en plakat i gruppen, som skal vise en felles løsning for oppgaven og som er bedre enn de individuelle svarene. Gruppen skal gi gode begrunnelser for tilnærmingen de velger å benytte og forklare hvordan de vet at de har funnet den korteste ruten. Tilslutt samler man klassen og diskuterer de ulike tilnærmingene og eventuelle beregninger gruppene har kommet fram til.
Etterarbeid:
Som etterarbeid til opplegget kan en gi elevene et refleksjonsskjema, der de svarer på spørsmål om hva fordelen og ulempen med denne type opplegg var for dem og hvordan det individuelle arbeidet var sammenlignet med gruppearbeidet. Dette skjemaet kan hjelpe læreren til å reflektere selv over erfaringen ved å bruke slike problemløsende oppgaver. I tillegg anbefales det at læreren i etterkant av undervisningsopplegget reflekterer rundt hva som gikk bra under utførelsen av opplegget, hvordan responsen fra elevene var og hva en som lærer ville gjort annerledes neste gang en utfører dette eller et annet opplegg (Mathematics Assessment Resource Service, 2013). Dette for å kunne forbedre egen undervisning og kunne utvikle seg som lærer.
Til ettertanke
Vi tenker at læreren ikke trenger å ha gjennomført problemløsning i undervisningen tidligere, men at h*n har kjennskap til problemløsningsstrategier som elevene kommer med. For at undervisningsopplegget skal kunne fungere optimalt må en ta hensyn til ulike forutsetninger. Læreren bør sette seg grundig inn i undervisningsopplegget, slik at h*n har best mulig oversikt over hvordan opplegget skal gjennomføres, hvilke ulike løsningsforslag elevene kan komme med, hvilke misforståelser elevene kan ha til opplegget og hvilke spørsmål elevene kan komme med underveis. Ved at læreren får elevene til å levere inn deres løsningsforslag på oppgaven før undervisningsøkten skal gjennomføres, kan dette hjelpe læreren til å tilrettelegge timen for elevene og en bedre forutsetning til en god gjennomføring av opplegget. Læreren må også tenke gjennom hvilke svar en kan gi elevene underveis, slik at en ikke gir dem løsningene på oppgaven, men lar elevene komme frem til ulike løsninger selv. Det er viktig for elevene at de har muligheten til å bli utfordret gjennom slike oppgaver, men også at de utfordrer seg selv ved å selv komme frem til løsningsmetoder. Gjennom opplegget er lærerens rolle å legge merke til de ulike tilnærmingene elevene har til oppgaven, samt støtte deres problemløsningsstrategier og bidra til å utvikle disse videre.
Vi mener at gjennom å benytte seg av denne type undervisningsopplegg vil læringsmiljøet i klassen utvikle seg og øke “scoren” innenfor de ulike dimensjonene i Tru Math gjennom undervisningsopplegget. I tillegg til at elevene gjennom denne problemløsningsoppgaven går gjennom problemløsningsprosessens ulike steg som er med til å bidra at de kan få en økende forståelse for temaet i oppgaven, som her omhandler geometri. Dette vil være med å bidra at elevene opparbeider seg en relasjonell forståelse om temaet. Slik at elevene gjennom opplegget opparbeider seg en bedre forståelse for målet for økta, nemlig å utvikle/tilegne seg kunnskap og forståelse for Pytagoras`setning og se hvordan en kan benytte seg av dette til å løse problemer i hverdagen.
Vi mener at problemløsning er viktig for at elevene skal kunne utvikle relasjonell forståelse i matematikk, men at utviklingen av denne forståelsen er avhengig av hvordan læreren utfører undervisningen. Derfor er det viktig at læreren vet hva fokuset for undervisningen bør være, slik at elevene har best mulig forutsetning for læring og utvikling av sin matematiske forståelse. Vi vil dermed avslutte med et sitat som vi tenker alle lærere bør ha i minnet når de planlegger sin undervisning.
«Improving teaching is not easy, but knowing what to focus on can be a big help»
(Schoenfeld mfl., 2016, s.3)
Kildehenvisning
Battista, M. T. (2007). “The development of geometric thinking and spatial thinking” In F. K. Lester (ed.). Second handbook of research on mathematics teaching and learning. (p. 843-908). Charlotte, N. C.: Information Age.
Lesh, L & Zawojweski (2007). “Problem solving and modeling”. In F. K. Lester (ed.). Second handbook of research on mathematics teaching and learning. (p. 763-804). Charlotte, N. C.: Information Age.
Mathematics Assessment Resource Service (2016). Finding the Shortest Route: A Schoolyard Problem. Hentet 02.10.2017: http://map.mathshell.org/lessons.php?unit=8305&collection=8&redir=1
Mathematics Assessment Resource Service (2013). A Brief Guide to teachers and administrators. University of Nottingham & UC Berkeley. Hentet 12.10.2017 fra:
Scoenfeld, A. H., Floden, R. E., & the Algebra Teaching Study and Mathematics Assessment Project (2014). An introduction to the TRU Math Dimensions. Berkeley, CA & E. Landing, MI: Graduate School of Education, University of California, Berkeley & College of Education, Michigan State University.
Schoenfeld, A. H. & the Teaching for Robust Understanding Project (2016). An Introduction to the Teaching for Robust Understanding (TRU) Framework. Berkeley, CA: Graduate School of Education.
Skemp, R. R. (1976). Relational Understanding and Instrumental Understanding. Mathematics teaching.
Utdanningsdirektoratet (2013). Læreplan i matematikk. Hentet 06.10.2017 fra: http://data.udir.no/kl06/MAT1-04.pdf
Bilde 1: The five dimensions of mathematically powerful classroom. Hentet 11.10.2017 fra “An introduction to the TRU Math dimensions”.
Bilde 2: Steps to solve a problem. Hentet 11.10.2017 fra:
Bilde 3: A schoolyard problem. Hentet 02.10.2017 fra: http://map.mathshell.org/lessons.php?unit=8305&collection=8&redir=1
Kommentarer
Legg inn en kommentar